The Creation Positional Numbers
The next one in the list of the most important events in ancient Babylonia is the creation of positional numbers. The concept of positional numbers, which refers to the importance of a digit based on both the digit and its position, was initially introduced by the Babylonians. They either employed the base-60 system or the sexagesimal system. Calculations were made simpler because the number 60 had several divisors. The division of time into 60 seconds in a minute and 60 minutes in an hour reflects this method even today. Positional numbers made it simpler to answer arithmetic issues, especially since zero was not a concept in Babylonian mathematics. The Babylonians were however aware of the void following nine. Their positional number system was regarded as their finest accomplishment, and it's believed that the sophisticated Babylonian number system also served as inspiration for the Greeks.
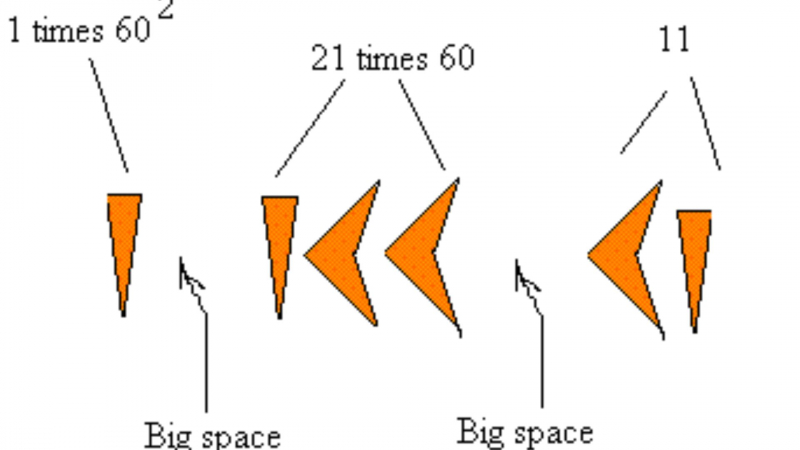
The value of a specific digit depends on both the digit itself and its position within the number, therefore the Babylonian system is recognized as the first known positional numeral system. This was a very significant invention since calculations can be more challenging in non-place-value systems where each power of a base (e.g., 10, 100, 1000, etc.) is represented by a different symbol. The 59 non-zero digits were represented by just two symbols. In a sign-value notation very reminiscent of Roman numerals, these symbols and their values were joined to produce a digit. To represent a place without value, like the contemporary zero, a space was left. Later, the Babylonians created a symbol to depict this void. The location of the units had to be deduced from context because they lacked a symbol to act as a radix point.
They used internal decimal to represent their digits, so it was clear that their system used internal decimal, but it wasn't really a mixed-radix system of bases 10 and 6 since the ten sub-base was only used to simplify the representation of the large set of digits required, while the place-values in a digit string were consistently 60-based and the arithmetic required to work with these digit strings was correspondingly sexagesimal. Even though both of these systems are truly mixed radix, the legacy of the sexagesimal is still there today in the shape of degrees, minutes, and seconds in trigonometry and the measurement of time.