Top 10 Best Books On Differential Equations
A differential equation is a mathematical equation that connects one or more unknown functions and their derivatives. In applications, functions are used to ... read more...represent physical values, derivatives are used to describe their rates of change, and differential equations define the relationship between the two. Because such relationships are widespread, differential equations serve an important role in many fields, including engineering, physics, economics, and biology. If you wish to learn differential equations, we recommend the best books on differential equations listed below.
-
In 1891, Silvanus P. Thompson was elected to the Royal Society. He authored a number of technical books and manuals on electricity, magnetism, dynamos, and optics, as well as several popular biographies of notable scientists.
Martin Gardner has published multiple book reviews for The New York Review of Books and has been a columnist for Scientific American for over twenty-five years. Calculus Made Easy and When You Were a Tadpole and I Were a Fish are two of his publications.
Silvanus P. Thompson and Martin Gardner's Calculus Made Easy has long been the most popular calculus primer. This major edition of the classic math textbook makes the subject even more understandable to students of all levels. Calculus Made Easy has been extensively updated for the modern reader, with a new introduction, three new chapters, modernized language and procedures throughout, and an appendix of hard and interesting practice problems.
This traditional calculus primer has been turned into a modern masterpiece that presents the timeless fundamentals of calculus in a contemporary and user-friendly manner in one of the most important popular math publications of the decade. Martin Gardner, Scientific American's "Mathematical Games" columnist for almost a quarter-century, is the ideal mathematician to make calculus accessible once more.
Calculus, while commonly regarded as the most difficult topic faced by a math student, does not have to be insurmountable. Calculus Made Easy was written about ninety years ago by Silvanus P. Thompson to demonstrate that differential and integral calculus is not at all difficult. Thompson believed that once a reader understood the fundamental ideas of differentiation and integration, the remainder of calculus would fall into place. His entire success is evidenced by the book's ongoing popularity over the years.
Gardner has extensively updated Calculus Made Easy since 1921 to incorporate contemporary changes in method and vocabulary, written a long prologue and three new introductory chapters, and included more than twenty recreational problems for practice and fun.
Calculus Made Easy, already the best primer for the general reader, has become even more approachable and enlightening in the skillful hands of one of the twentieth century's finest minds.
Author: Silvanus P. Thompson and Martin Gardner
Link to buy: https://www.amazon.com/Calculus-Made-Easy-Silvanus-Thompson/dp/0312185480/
Ratings: 4.5 out of 5 stars (from 514 reviews)
Best Sellers Rank: #11,299 in Books
#2 in Differential Equations (Books)
#4 in Mathematics Reference (Books)
#6 in Calculus (Books)

https://www.amazon.com/ 
https://www.amazon.com/ -
Daniel Fleisch is an Associate Professor of Physics at Wittenberg University in Ohio. Radar cross-section measurement, radar system analysis, and ground-penetrating radar are among his research interests. He belongs to the American Physical Society (APS), the American Association of Physics Teachers (AAPT), and the Institute of Electronic and Electrical Engineers (IEEE).
Maxwell's equations are four of science's most influential equations. Each equation is the focus of a whole chapter in A Student's Guide to Maxwell's Equations, making it an excellent resource for undergraduate and graduate courses in electromagnetism and electromagnetics. The book is one of the best books on differential equations.
Four of the most influential equations in physics are Gauss' law for electric fields, Gauss' law for magnetic fields, Faraday's law, and the Ampere Maxwell law. Each equation is the focus of a complete chapter in this student handbook, with thorough, plain language explanations of the physical significance of each symbol in the equation, for both the integral and differential forms. The final chapter demonstrates how Maxwell's equations can be coupled to generate the wave equation, which serves as the foundation for the electromagnetic theory of light. This book is an excellent resource for electromagnetism and electromagnetics courses at the undergraduate and graduate levels.
Author: Daniel Fleisch
Link to buy: https://www.amazon.com/Students-Guide-Maxwells-Equations-Guides/dp/0521701473/
Ratings: 4.7 out of 5 stars (from 558 reviews)
Best Sellers Rank: #54,043 in Books
#7 in Differential Equations (Books)
#17 in Physics (Books)
#18 in Mathematical Physics (Books)
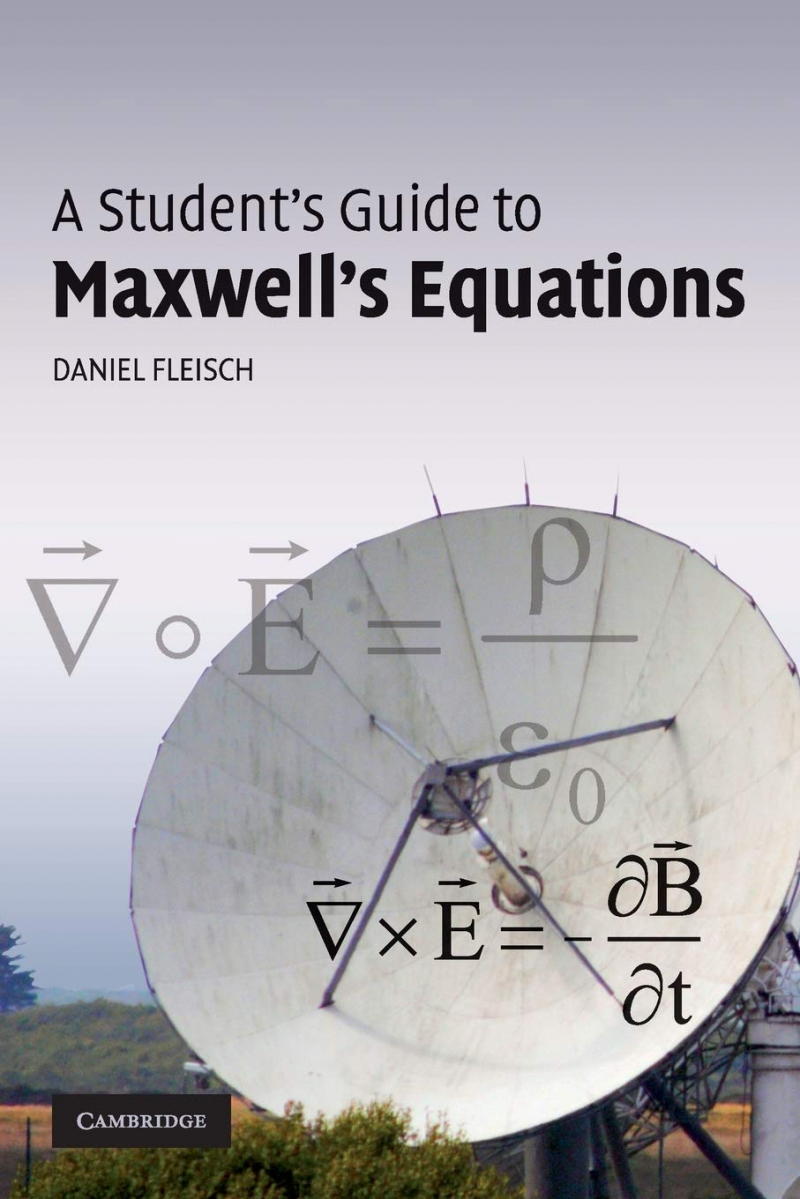
amazon.co.uk 
amazon.co.uk -
Dan Hamilton earned a Bachelor of Science in Electrical Engineering from Oklahoma State University and a Master of Science in Electrical Engineering from the University of Texas at Austin. As a visiting professor at the University of Oklahoma's Department of Mathematics and as a faculty member at Rose State College's Department of Engineering Technology in Midwest City, Oklahoma, he taught a variety of math and engineering courses. He is currently working in the field of aeronautical technology and has multiple technical articles to his credit.
The author's primary goal in publishing this book is to provide a basic and uncomplicated approach for teaching arithmetic that demystifies the topic and makes math accessible to everybody. As arithmetic becomes increasingly vital in our high-tech society, the author hopes that this simplified teaching style will pique the interest of math students of all ages.
Why do you select Calculus 1 - Differentiation and Integration?
- The most authoritative text and student reference on introductory calculus available.
- Discover operations involving sequences, series, limits, factorials, differentiation, integration, and more.
- Over 1,900 problems with detailed solution checking
- Self-teaching design effective for 12th grade through college level and adults
- Provides a strong foundation for students progressing to advanced college calculus
- Unique step-by-step approach makes math easy to learn and stimulates desire to learn
- Student-tested solutions found exclusively in Hamilton Education Guides
- Provides a lifetime methodology for problem solving and reduces math anxiety
Author: Dan Hamilton
Link to buy: https://www.amazon.com/Calculus-Differentiation-Integration-Hamilton-Education-ebook/dp/B07BPHW4VL/
Ratings: 4.6 out of 5 stars (from 28 reviews)
Best Sellers Rank: #94,679 in Kindle Store
#1 in Differential Equations (Kindle Store)
#6 in Calculus (Kindle Store)
#8 in Differential Equations (Books)

https://www.amazon.com/ 
https://www.amazon.com/ -
Algebra is a significant subfield of mathematics if only for its variety. You'd be hard pressed to identify a single field of mathematics taught after algebra where algebra isn't used in practically every case. The most general and often used definition of algebra is the study of mathematical symbols and the manipulation of these symbols.
Aside from numbers and operation symbols, mathematical symbols are one of the most fundamental aspects of mathematics, making the study of these symbols one of the most important topics in mathematics. To that goal, Algebra 1 Workbook covers some of the most significant subjects in algebra.
These include but are not limited to the following: understanding integers and basic operations, inequalities and one-step operations; fractions and factors; the main rules of arithmetic; linear equations in the coordinate plane, expressions, equations and functions; real numbers; solving linear equations; visualizing linear functions, linear equations, linear inequalities, systems of linear equations and inequalities; exponents and exponential function; polynomials, quadratic equations, radical expression, radical equations, rational expressions; and finally, intermediate topics in algebra.
Author: Richard Carter
Link to buy: https://www.amazon.com/Algebra-Workbook-Self-Teaching-Exercises-Explained/dp/1790340098/
Ratings: 4.2 out of 5 stars (from 937 reviews)
Best Sellers Rank: #60,972 in Books
#9 in Differential Equations (Books)
#15 in Intermediate Algebra (Books)

https://www.amazon.com/ 
https://www.amazon.com/ -
This uncommonly well-written and effectively arranged introductory course offers a thorough examination of ordinary differential equations – equations that explain the connection between variables and their derivatives. Morris Tenenbaum of Cornell University and Harry Pollard of Purdue University introduce and explain complex, critically essential concepts to undergraduate students of mathematics, engineering, and the sciences in a deceptively simple, step-by-step method that never loses mathematical rigor.
Ordinary Differential Equations opens with a part that discusses the origins of differential equations, defines basic concepts, and outlines the general solution of a differential equation—the solution that contains every solution of such an equation. Following sections include topics such as integrating factors, dilution and accretion problems, complex number algebra, linearization of first order systems, Laplace Transforms, Newton's Interpolation Formulas, and Picard's Method of Successive Approximations.
There are two outstanding chapters in the book: one on series methods of solving differential equations and the other on numerical methods of solving differential equations. The first covers the Legendre Differential Equation, Legendre Functions, Legendre Polynomials, Bessel Differential Equation, and Laguerre Differential Equation. Every term is described clearly throughout the book, and every theorem is lucidly and thoroughly examined, and there is an amazing balance between differential equation theory and application. Ordinary Differential Equations' relevance as a classroom work for undergraduate students and teaching professionals is enhanced by a wealth of solved problems and practice exercises. The book closes with an in-depth analysis of existence and uniqueness theorems for various differential equations, as well as an introduction to determinant theory and Wronskians theorems.
Author: Morris Tenenbaum and Harry Pollard
Link to buy: https://www.amazon.com/Ordinary-Differential-Equations-Dover-Mathematics/dp/0486649407/
Ratings: 4.5 out of 5 stars (from 498 reviews)
Best Sellers Rank: #62,394 in Books
#10 in Differential Equations (Books)
#25 in Calculus (Books)

amazon.co.uk 
ebay.com -
Partial Differential Equations for Scientists and Engineers by Stanley J. Farlow is one of Dover's most extensively used textbooks.
Most physical phenomena, whether in fluid dynamics, electricity, magnetism, mechanics, optics, or heat transport, may be generalized using partial differential equations. Such equations are essential in mathematical physics. Although these equations can be simplified to become ordinary differential equations, the comprehensive description of physical systems is found in the general topic of partial differential equations.
Partial Differential Equations for Scientists and Engineers really useful text demonstrates how to formulate a partial differential equation from a physical situation (building the mathematical model) and solve the equation (along with initial and boundary conditions). This well written book provides realistic, practical coverage of diffusion-type problems, hyperbolic-type problems, elliptic-type problems, and numerical and approximate approaches for advanced undergraduate and graduate students, as well as professionals working in the applied sciences. Each chapter includes a selection of relevant problems (with solutions) and ideas for further study. It is considered one of the best books on differential equations.
Author: Stanley J. Farlow
Link to buy: https://www.amazon.com/Differential-Equations-Scientists-Engineers-Mathematics/dp/048667620X/
Ratings: 4.5 out of 5 stars (from 363 reviews)
Best Sellers Rank: #66,336 in Books
#6 in Civil Engineering (Books)
#12 in Differential Equations (Books)
#132 in Civil & Environmental Engineering

amazon.in 
amazon.in -
Arthur Benjamin has a PhD from Johns Hopkins University and is a mathematics professor at Harvey Mudd College. He wrote the book The Secrets of Mental Math.
The Magic of Math is the math book you wish you could have gotten in school. This book revels in key mathematical fields such as arithmetic, algebra, geometry, and calculus, as well as Fibonacci numbers, infinity, and, of course, mathematical magic tricks, using a delightful assortment of examples ranging from ice cream scoops and poker hands to measuring mountains and making magic squares. Arthur Benjamin, known around the world as the "mathemagician," combines mathematics with magic to make the topic appealing to both math fans and math skeptics.
The Magic of Math offers a fast-paced tour of 12 main themes that range from basic mathematics to the nuances of infinite sums.... All of these themes are approached by Benjamin with the purpose of stressing the wonder and enchantment inherent in them but still giving the reader a feeling of the mathematics hidden behind the magician's sleeve.... The book contains a bewildering diversity of mathematical delights. But here, once the mathemagician has completed his sleight-of-hand, we have the pleasure of peering behind the curtain to see how all those tricks are performed.
Author: Arthur Benjamin
Link to buy: https://www.amazon.com/Magic-Math-Solving-Figuring-Out/dp/0465096212/
Ratings: 4.5 out of 5 stars (from 307 reviews)
Best Sellers Rank: #109,877 in Books
#6 in Combinatorics (Books)
#8 in Analytic Geometry (Books)
#11 in Mathematical Infinity

https://www.amazon.com/ 
https://www.amazon.com/ -
The title of this book is meant to be a challenge rather than a promise. Nobody can guarantee that you will be able to study differential equations in 24 hours. That is all up to you.
Differential Equations in 24 Hours makes it feasible to master basic differential equations in the shortest period of time possible. It features a concise presentation style and the appropriate number of exercises and examples—not too many, nor too few. Appendix 1 has a detailed explanation of all of the solutions to the exercises. This enables for reinforcement learning and success verification. Biographical biographies of notable mathematicians are given to provide further incentive; however, they can be omitted to save even more time. Italicized text indicates stuff that can be skipped. The material offered here is equivalent to that presented in the author's junior-level differential equations course at the University of Colorado Denver. It evolved from his previous book, Shortcut to Ordinary Differential Equations.
The current book, which has been somewhat expanded and includes all of the solutions, covers essentially the same themes as a junior-level differential equations course that the author completed at Indiana University-Purdue University Indianapolis. The book is among the best books on differential equations.
Author: Scott Imhoff PhD
Link to buy: https://www.amazon.com/Differential-Equations-Hours-Solutions-Historical-ebook/dp/B019MB828Y/
Ratings: 4.4 out of 5 stars (from 128 reviews)
Best Sellers Rank: #163,572 in Kindle Store
#3 in Differential Equations (Kindle Store)
#15 in Differential Equations (Books)

twitter.com 
twitter.com -
Steven Holzner is an award-winning science, math, and technology author. He studied differential equations at MIT and Cornell University, where he earned his PhD. He has taught at both MIT and Cornell University, and his books include Physics For Dummies and Physics Workbook For Dummies.
Many basic rules of physics, chemistry, biology, and economics can be expressed as differential equations. This simple-to-understand guide explores the many applications of this mathematical tool and demonstrates how differential equations may help us comprehend our surroundings. Differential Equations For Dummies is a fantastic supplemental resource for other calculus classes, as well as science and engineering courses, and is the appropriate companion for a college differential equations course. It provides readers with step-by-step strategies, practical recommendations, numerous exercises, and clear, simple examples to help them enhance their differential equation-solving abilities and test results.
Learn how to:
- Differential equations should be classified.
- Utilize integrating elements to solve
- Use coefficients to your advantage.
- Use useful theorems
- Experiment with sophisticated approaches.
- In real life, use differential equations.
Author: Steven Holzner
Link to buy: https://www.amazon.com/Differential-Equations-Dummies-Steven-Holzner/dp/0470178140/
Ratings: 4.5 out of 5 stars (from 235 reviews)
Best Sellers Rank: #116,602 in Books
#16 in Differential Equations (Books)
#299 in Math Teaching Materials
#381 in Mathematics (Books)

amazon.co.uk 
itres.com -
C. Henry Edwards is an emeritus mathematics professor at the University of Georgia. He received his Ph.D. from the University of Tennessee in 1960 and recently retired after 40 years of classroom teaching (including calculus or differential equations almost every term) at the universities of Tennessee, Wisconsin, and Georgia, with a brief interlude as an Alfred P. Sloan Research Fellow at the Institute for Advanced Study (Princeton).
David E. Penney, University of Georgia, received his Ph.D. in 1965 from Tulane University (directed by Prof. L. Bruce Treybig) while teaching at the University of New Orleans. He has written research papers in number theory and topology, as well as textbooks on calculus, computer programming, differential equations, linear algebra, and liberal arts mathematics.
Through real-world applications, concepts, methods, and key subjects in elementary differential equations and linear algebra are covered.
Distinguished authors Edwards and Penney integrate key subjects in elementary differential equations with concepts and methods from elementary linear algebra in a modern introduction to differential equations and linear algebra. Differential Equations and Linear Algebra, renowned for its real-world applications and blend of algebraic and geometric methodologies, introduces you to mathematical modeling of real-world processes and provides the best problem sets of any differential equations and linear algebra course. The 4th Edition has a new computational and qualitative flavor that may be seen in the images, examples, puzzles, and applications. In addition, an Expanded Applications website with additional applications and programming tools is also available. The book is regarded as one of the best books on differential equations.
Author: David Calvis and Henry Edwards
Link to buy: https://www.amazon.com/Differential-Equations-Linear-Algebra-4th/dp/013449718X/
Ratings: 4.2 out of 5 stars (from 103 reviews)
Best Sellers Rank: #140,867 in Books
#23 in Differential Equations (Books)
#32 in Linear Algebra (Books)
#124 in Algebra & Trigonometry

https://www.amazon.com/ 
https://www.amazon.com/