Top 5 Interesting Facts about John Wallis
John Wallis (Latin: Wallisius; December 3, 1616 - November 8, 1703) was an English clergyman and mathematician who is credited with developing the ... read more...infinitesimal calculus. Here are the 5 interesting facts about John Wallis you should know.
-
One of the interesting facts about John Wallis is that John Wallis was born in Ashford, Kent. Ashford is a town in the English county of Kent. It is located on the Great Stour River at the southern or scarp edge of the North Downs, approximately 61 miles (98 kilometers) southeast of central London and 15.3 miles (24.6 kilometers) northwest of Folkestone via road. It has a population of 74,204 according to the 2011 census. The name is derived from the Old English æscet, which refers to a ford near a clump of ash trees. It has been a market town since the Middle Ages and still holds a regular market. He was the third of Reverend John Wallis and Joanna Chapman's five children. He began his education in a school in Ashford but was transferred to James Movat's school in Tenterden in 1625 due to a plague outbreak. Wallis was introduced to mathematics for the first time in 1631, at Felsted School (then known as Martin Holbeach's school in Felsted); he enjoyed math, but his study was erratic, because mathematics, at that time with us, was scarcely looked on as academic studies, but rather mechanical (Scriba 1970). Wallis learned to speak and write Latin at the Felsted school.
He was also fluent in French, Greek, and Hebrew by this point. He was sent to Emmanuel College, Cambridge, in 1632, with the intention of becoming a doctor. While there, he kept an act on the idea of blood circulation, which was considered to be the first time in Europe that this theory was openly maintained in a debate. His interests, on the other hand, were oriented toward mathematics. He got his Bachelor of Arts degree in 1637 and a Master's in 1640 and subsequently joined the priesthood. He was a nonvoting scribe at the Westminster Assembly from 1643 to 1649. In 1644, he was elected to a fellowship at Queens College, Cambridge, which he had to withdraw from due to his marriage.
en.wikipedia.org 
britannica.com -
It is a fact that he wrote the book “Arithmetica Infinitorum”. The most important of Wallis' works, Arithmetica Infinitorum, was published in 1656. The methods of analysis of Descartes and Cavalieri were systematized and enlarged in this treatise, however, several notions were susceptible to critique. After a brief introduction to conic sections, he went on to establish the conventional notation for powers, extending it beyond positive integers to rational numbers.
The generation and attributes of continuing fractions are also examined in this study, which was brought to light by Brouncker's use of these fractions. A few years later, in 1659, Wallis published a tract giving the solution to Blaise Pascal's puzzles on the cycloid. In this, he also explained how the principles outlined in his Arithmetica Infinitorum could be applied to the rectification of algebraic curves and provided a solution to the problem of rectifying the semicubical parabola, which was discovered in 1657 by his pupil William Neile. Since all attempts to rectify the ellipse and hyperbola had been ineffective, it was assumed that no curves could be rectified, as Descartes had emphatically stated. Evangelista Torricelli rectified the logarithmic spiral, which was the first curved line (other than the circle) whose length was calculated, but Neile and Wallis' application to an algebraic curve was innovative. Christopher Wren rectified the cycloid as the next curve to be rectified in 1658.

Arithmetica Infinitorum -Photo: maa.org 
Arithmetica Infinitorum -Photo: maa.org -
One of the interesting facts about John Wallis is that he is credited with coining the symbol ∞ for the concept of infinity. Wallis published a treatise on conic sections in 1655, which defined them analytically. This was the first book to consider and define these curves as curves of the second degree. It helped to dispel some of the misconceptions about René Descartes' work on analytic geometry. Wallis popularized the symbol ∞ of infinity in his Treatise on Conic Sections. "I suppose any plane (following the Geometry of Indivisibles of Cavalieri) to be made up of an infinite number of parallel lines, or as I would prefer, of an infinite number of parallelograms of the same altitude; (let the altitude of each one of these be an infinitely small part 1/∞ of the whole altitude, and let the symbol ∞ denote Infinity) and the altitude of all to make up the altitude of the figure", he wrote.
Infinity is defined as anything that is limitless, endless, or greater than any natural number. It is frequently represented by the infinity symbol ∞. Many philosophers have debated the philosophical nature of infinity since the time of the ancient Greeks. With the introduction of the infinity symbol and the infinitesimal calculus in the 17th century, mathematicians began to work with infinite series and what some mathematicians considered infinitely small quantities, but infinity remained associated with endless processes. As mathematicians struggled with the calculus foundation, it remained unclear whether infinity could be considered a number or magnitude, and if so, how. Georg Cantor expanded the mathematical study of infinity at the end of the nineteenth century by studying infinite sets and infinite numbers, demonstrating that they can be of various sizes. Infinity is a mathematical concept, and infinite mathematical objects, like any other mathematical object, can be studied, manipulated, and used.
The symbol of infinity -Photo: en.wikipedia.org 
Photo: twitter.com -
An interesting fact is that John Wallis is one of the greatest codebreakers. Wallis had been close to the Parliamentarian party throughout this time, possibly as a result of his exposure to Holbeach at Felsted School. He was of great practical assistance to them in deciphering Royalist dispatches. Despite the individual successes of mathematicians such as François Viète, the principles underlying cipher design and analysis were very poorly understood at the time. In contrast to systems based on a variable key, most ciphers were ad hoc methods relying on a secret algorithm. Wallis recognized that the latter was far more secure, even calling them "unbreakable," though he was not confident enough in this claim to encourage the disclosure of cryptographic algorithms. He was also concerned about foreign powers using ciphers, turning down Gottfried Leibniz's request in 1697 to teach Hanoverian students about cryptography.
Returning to London after being appointed chaplain at St Gabriel Fenchurch in 1643, Wallis joined the group of scientists that would later become the Royal Society. In 1647, he was finally able to pursue his mathematical interests, mastering William Oughtred's Clavis Mathematicae in a matter of weeks. He soon began to write his own treatises on a variety of topics, which he continued to do for the rest of his life. In England, Wallis published the first survey of mathematical concepts, in which he discussed the Hindu-Arabic system.

Felsted School -Photo: ru.linkedin.com 
St Gabriel Fenchurch -Photo: en.wikipedia.org -
One of the interesting facts about John Wallis is that he is commonly credited with proving the Pythagorean theorem with similar triangles. Six centuries earlier, Thabit Ibn Qurra (AD 901), an Arab mathematician, had produced a generalization of the Pythagorean theorem applicable to all triangles. It's safe to assume that Wallis was aware of Thabit's work.
Wallis was also influenced by the works of Islamic mathematician Sadr al-Tusi, particularly by al-Tusi's book written in 1298 on the parallel postulate. His father's ideas inspired the book, which presented one of the earliest arguments for a non-Euclidean hypothesis equivalent to the parallel postulate. After reading this, Wallis wrote about his thoughts as he developed his own ideas about the postulate, attempting to prove it with similar triangles as well.
He discovered that Euclid's fifth postulate is equivalent to the one that is now known as the "Wallis postulate" after him. According to this postulate, "On a given finite straight line it is always possible to construct a triangle similar to a given triangle" This result was part of a trend that attempted to deduce Euclid's fifth postulate from the other four, which is now known to be impossible. Unlike other authors, he recognized that the four first postulates did not guarantee the unbounded growth of a triangle.
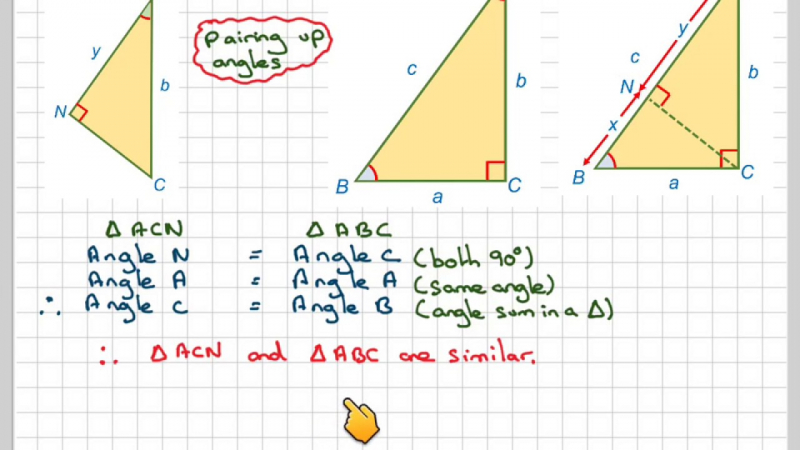
Proof of Pythagoras theorem using similar triangles -Photo: youtube.com 
Thabit Ibn Qurra -Photo: steamdaily.com


























