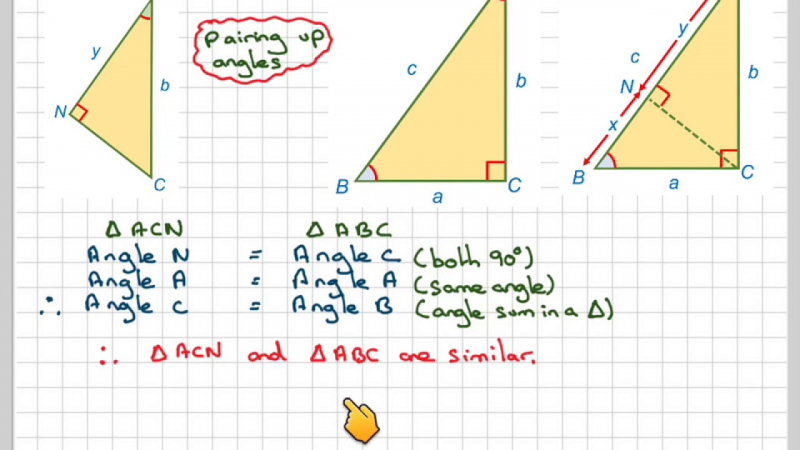
He is commonly credited with proving the Pythagorean theorem with similar triangles

One of the interesting facts about John Wallis is that he is commonly credited with proving the Pythagorean theorem with similar triangles. Six centuries earlier, Thabit Ibn Qurra (AD 901), an Arab mathematician, had produced a generalization of the Pythagorean theorem applicable to all triangles. It's safe to assume that Wallis was aware of Thabit's work.

Wallis was also influenced by the works of Islamic mathematician Sadr al-Tusi, particularly by al-Tusi's book written in 1298 on the parallel postulate. His father's ideas inspired the book, which presented one of the earliest arguments for a non-Euclidean hypothesis equivalent to the parallel postulate. After reading this, Wallis wrote about his thoughts as he developed his own ideas about the postulate, attempting to prove it with similar triangles as well.

He discovered that Euclid's fifth postulate is equivalent to the one that is now known as the "Wallis postulate" after him. According to this postulate, "On a given finite straight line it is always possible to construct a triangle similar to a given triangle" This result was part of a trend that attempted to deduce Euclid's fifth postulate from the other four, which is now known to be impossible. Unlike other authors, he recognized that the four first postulates did not guarantee the unbounded growth of a triangle.