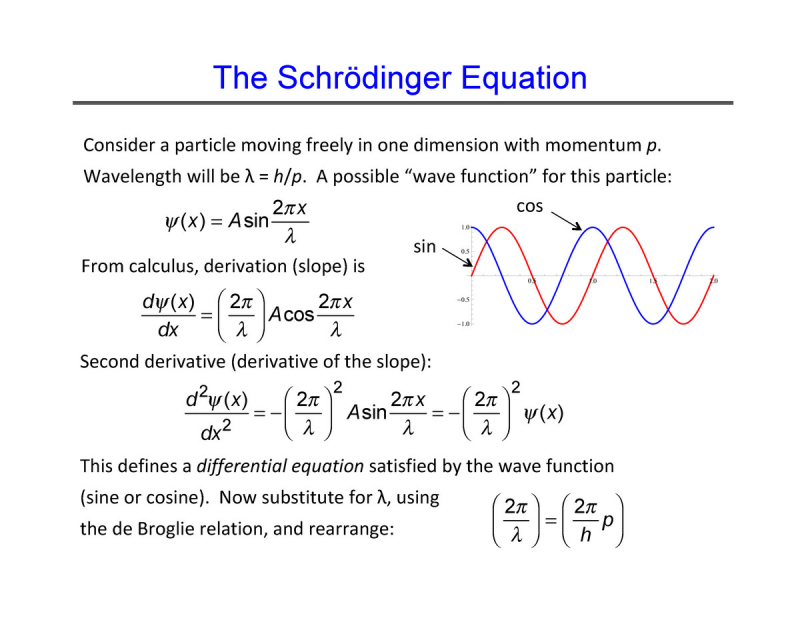
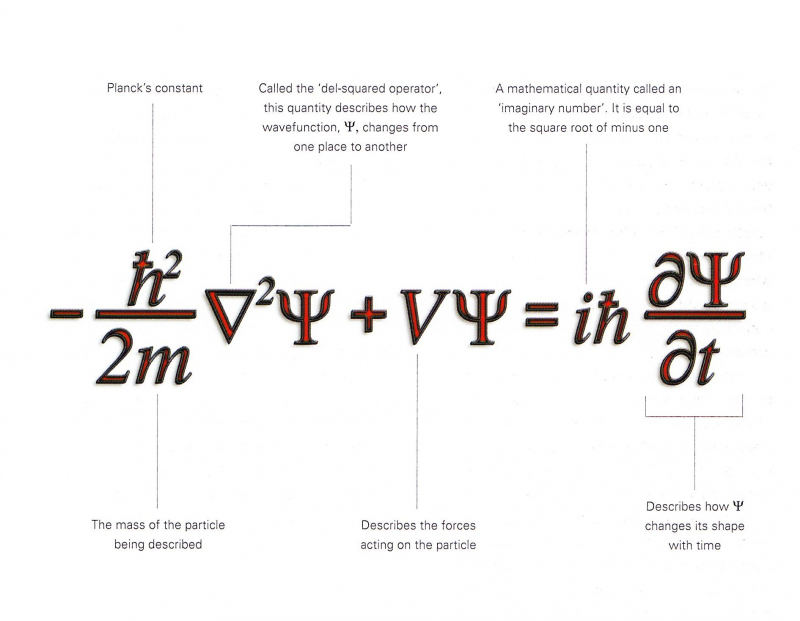One of his most notable works is the Schrödinger wave equation.

The Schrödinger Equation was one of Erwin Schrödinger's most important contributions. Schrödinger equation is a linear partial differential equation that is used to explain the wave or state function of a quantum-mechanical system, one of the interesting facts about Erwin Schrödinger.

The finding was discovered by Schrödinger in 1925, and it was this that helped him earn the Nobel Prize less than ten years later. Significant progress in the field of quantum physics was made possible by this finding.

One of the most significant phases of Schrödinger's physics career would be the six years he spent as a professor at the University of Zurich. Schrödinger discovered Louis de Broglie's work in 1925 while immersing himself in a variety of theoretical physics studies. De Broglie had put out a wave mechanics hypothesis in his 1924 thesis. This piqued Schrödinger's curiosity about why an electron in an atom would travel as a wave. The following year, he published a ground-breaking study that highlighted the concept of the Schrödinger wave equation.

Schrödinger described the motions of electrons in terms of wave mechanics as opposed to particle jumps, building on de Broglie's thesis and Niels Bohr's atomic model. He gave scientists a way of thinking that was widely adopted, used in many publications, and served as a key tenet of quantum theory. While the majority of theoretical physicists shared ground-breaking discoveries in their 20s, Schrödinger made this discovery in his late 30s.